Question

The height h of an object thrown from the top of a ski lift 1240 feet high after t seconds is h=-16t2 +32t+1240. For what times is the height of the object at least 1000 feet?

←
The height of the object is at least 1000 feet from seconds to seconds.

Answer 1

Check the picture below.

so the parabolic path of the object is more or less like the one shown below in the picture, now this object has an initial of 1240 ft, as it gets thrown from the ski lift, so from 0 seconds is already higher than 1000 feet.

`h=-16t^2+32t+1240\hspace{5em}\stackrel{\textit{a height of 1000 ft}}{1000=-16t^2+32t+1240} \\\\\\ 0=-16t^2+32t+240\implies 16t^2-32t-240=0\implies 16(t^2-2t-15)=0 \\\\\\ t^2-2t-15=0\implies (t-5)(t+3)=0\implies t= \begin{cases} ~~ 5 ~~ \textit{\LARGE \checkmark}\\ -3 ~~ \bigotimes \end{cases}`

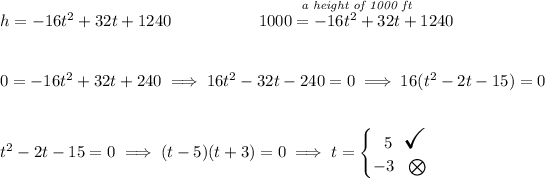
now, since the seconds can't be negative, thus the negative valid answer in this case is not applicable, so we can't use it.

So the object on its way down at some point it hit 1000 ft of height and then kept on going down, and when it was above those 1000 ft mark happened between 0 and 5 seconds.