Question

Joshua cuts off an isosceles right triangle from each corner of a square piece of paper in such a way that the remaining piece is a rectangle. In the picture to the right the removed triangles are shaded. Find the sum of the areas of the removed tirangles if the length of the diagonal of the remaing rectangle is 10cm.

RSM problem

Answer 1

50 cm²

Explanation:

An isosceles right triangle is a triangle with two sides of equal length (legs) and one right angle.

Let "x" be the leg of the smaller isosceles right triangle.

Let "y" be the leg of the larger isosceles right triangle.

The smaller isosceles right triangles are congruent, and the larger isosceles right triangles are congruent. Therefore:

• The sum of the area of the two smaller triangles is x².
• The sum of the area of the two larger triangles is y².

Therefore, the total area of the removed triangles is x² + y².

As the ratio of the lengths of the two congruent sides (legs) to the length of the hypotenuse of an isosceles right triangle is 1 : 1 : √2, then:

• The shorter side of the rectangle is x√2.
• The longer side of the rectangle is y√2.

The diagonal of the rectangle, d = 10, is the hypotenuse of two congruent triangles with legs x√2 and y√2.

Using Pythagoras Theorem, we can create an equation using this information:

`\text{(leg\;1)}^2+\text{(leg\;2)}^2=\text{hypotenuse}^2`

`(x√(2))^2+(y√(2))^2=10^2`

`2x^2+2y^2=100`

`x^2+y^2=50`

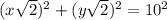
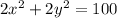
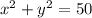
As we have already determined that the total area of the removed triangles is x² + y², then the sum of the areas of the removed triangles is 50 cm².