To express the given expression as a natural number, let's simplify it step by step.
The expression is:
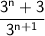
We can rewrite the numerator as:
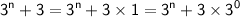
Now, let's combine the terms in the numerator:

Next, let's rewrite the denominator as:
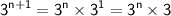
Now, substituting the rewritten numerator and denominator back into the expression, we have:
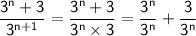
Simplifying further, we get:
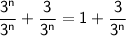
So, the expression
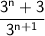 simplifies to
simplifies to
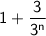 , which can be expressed as a natural number.
, which can be expressed as a natural number.