Question

Sketch two periods of the graph of the function h(x)=5sec(π4(x+3)). Identify the stretching factor, period, and asymptotes.

Stretching factor =
Period: P=
What are the asymptotes of the function on the domain [−P,P].
Asymptotes: x=

Answer 1

To sketch the graph of the function
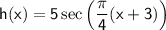`\displaystyle\sf h(x)=5\sec\left((\pi)/(4)(x+3)\right)`, let's first analyze its properties.

The stretching factor of the secant function
`\displaystyle\sf \sec(x)` is 1, which means it doesn't affect the shape of the graph.

Next, we can determine the period
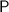`\displaystyle\sf P` of the function. The period of the secant function is
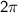`\displaystyle\sf 2\pi`, but in this case, we have a coefficient of
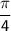`\displaystyle\sf (\pi)/(4)` multiplying the variable
`\displaystyle\sf x`. To find the period, we can set the argument of the secant function equal to one period, which gives us:

`\displaystyle\sf (\pi)/(4)(x+3)=2\pi`

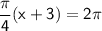
Solving for
`\displaystyle\sf x`:

`\displaystyle\sf x+3=8`

`\displaystyle\sf x=5`

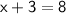
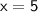
Therefore, the period
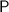`\displaystyle\sf P` is
`\displaystyle\sf 5`.

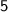Now let's determine the asymptotes. The secant function has vertical asymptotes where the cosine function, its reciprocal, is equal to zero. The cosine function is zero at
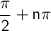`\displaystyle\sf (\pi)/(2)+n\pi` for integer values of
`\displaystyle\sf n`. In our case, since the argument is
`\displaystyle\sf (\pi)/(4)(x+3)`, we solve:

`\displaystyle\sf (\pi)/(4)(x+3)=(\pi)/(2)+n\pi`

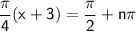
Solving for
`\displaystyle\sf x`:

`\displaystyle\sf x+3=2+4n`

`\displaystyle\sf x=2+4n-3`

`\displaystyle\sf x=4n-1`

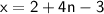
Therefore, the asymptotes on the domain
`\displaystyle\sf [-P,P]` are
`\displaystyle\sf x=4n-1`, where
`\displaystyle\sf n` is an integer.

To sketch the graph, we can plot a few points within two periods of the function, and connect them smoothly. Let's choose points at
`\displaystyle\sf x=0,1,2,3,4,5,6,7`:

Plotting these points and connecting them smoothly, we obtain a graph that oscillates between positive and negative values, with vertical asymptotes at
`\displaystyle\sf x=4n-1` for integer values of
`\displaystyle\sf n`.

The graph of
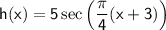`\displaystyle\sf h(x)=5\sec\left((\pi)/(4)(x+3)\right)` with two periods is as follows:

```

| /\

6 |-+----------------------+-+-------\

| | \

5 |-+---------+ | +-------\

| | / \

4 | | / \

| | / \

3 | \ / \

| \ / \

2 | \ / \

| \ / \

1 + \ / \

| | \

0 |-+--+--+--+--+--+--+--+--+--+--+--+--+--+--+--+--+--+-\

-4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10

```

Stretching factor:
`\displaystyle\sf 1`

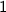
Period
`\displaystyle\sf P`:
`\displaystyle\sf 5`

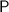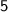
Asymptotes:
`\displaystyle\sf x=4n-1` for integer values of
`\displaystyle\sf n`