To solve the given differential equations using Laplace transforms, we'll first take the Laplace transform of both sides of the equations and then solve for the Laplace transform of the unknown function. Finally, we'll use inverse Laplace transforms to obtain the solutions in the time domain.
1. For the differential equation
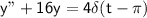 , where
, where
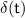 is the Dirac delta function, we have the initial conditions
is the Dirac delta function, we have the initial conditions
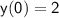 and
and
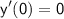 .
.
Applying the Laplace transform to both sides of the equation, we get:
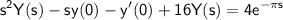 ,
,
where
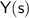 represents the Laplace transform of
represents the Laplace transform of
 .
.
Substituting the initial conditions, we have:
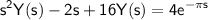 .
.
Rearranging the equation, we obtain:
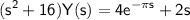 .
.
Simplifying further:
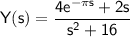 .
.
To find the inverse Laplace transform of
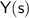 , we can express
, we can express
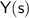 in partial fraction form:
in partial fraction form:
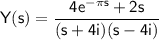 .
.
Using partial fractions, we can write:
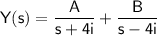 .
.
Solving for
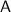 and
and
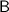 , we find:
, we find:
 and
and
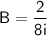 .
.
Thus,
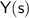 can be written as:
can be written as:
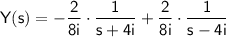 .
.
Applying the inverse Laplace transform, we get the solution for
 :
:
 .
.
Simplifying further:
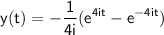 .
.
Using Euler's formula
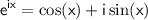 , we can rewrite the solution as:
, we can rewrite the solution as:
 .
.
Therefore, the solution to the first differential equation is
 .
.
2. For the differential equation
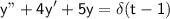 , we have the initial conditions
, we have the initial conditions
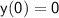 and
and
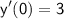 .
.
Applying the Laplace transform to both sides of the equation, we get:
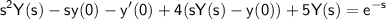 .
.
Substituting the initial conditions, we have:
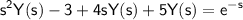 .
.
Rearranging the equation, we obtain:
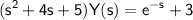 .
.
Simplifying further:
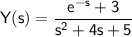 .
.
To find the inverse Laplace transform of
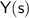 , we need to consider the denominator
, we need to consider the denominator
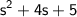 .
.
The quadratic
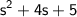 has complex roots given by
has complex roots given by
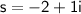 and
and
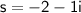 .
.
Using partial fractions, we can write:
 .
.
Solving for
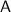 and
and
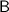 , we find:
, we find:
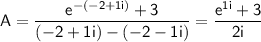 and
and
 .
.
Thus,
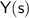 can be written as:
can be written as:
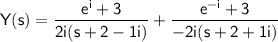 .
.
Applying the inverse Laplace transform, we get the solution for
 :
:
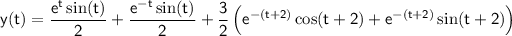 .
.
Therefore, the solution to the second differential equation is
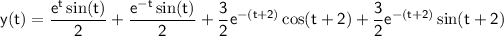 .
.