To find the determinant of the given matrix using expansion by cofactors, we can start by selecting any row or column. Let's choose the first row for this example.
The formula for expanding the determinant by cofactors along the first row is:
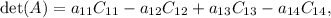
where
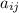 represents the elements of the matrix and
represents the elements of the matrix and
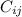 represents the cofactors.
represents the cofactors.
Given matrix
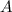 :
:
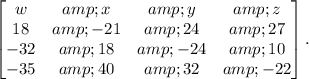
Expanding along the first row, we have:
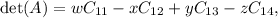
where
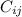 is the cofactor of
is the cofactor of
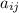 .
.
The cofactor of
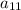 is given by the determinant of the 3×3 matrix obtained by removing the first row and first column:
is given by the determinant of the 3×3 matrix obtained by removing the first row and first column:
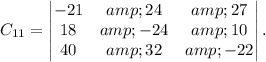
The cofactor of
 is given by the determinant of the 3×3 matrix obtained by removing the first row and second column:
is given by the determinant of the 3×3 matrix obtained by removing the first row and second column:
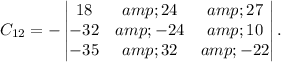
The cofactor of
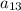 is given by the determinant of the 3×3 matrix obtained by removing the first row and third column:
is given by the determinant of the 3×3 matrix obtained by removing the first row and third column:
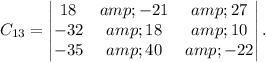
The cofactor of
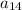 is given by the determinant of the 3×3 matrix obtained by removing the first row and fourth column:
is given by the determinant of the 3×3 matrix obtained by removing the first row and fourth column:
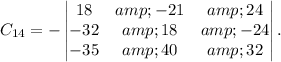
Calculating the determinants of the corresponding matrices, we find:
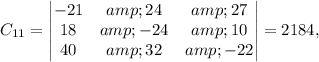
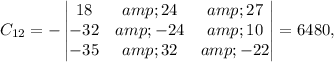
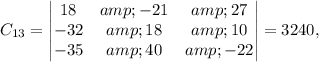
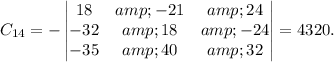
Now, substituting these values back into the expansion formula, we have:
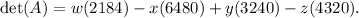
Hence, the determinant of the given matrix is:
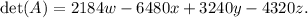

♥️
