Question

The signal x(t) = u(t) + 5u(t-1)-2u(t-2) has an average power of 8W. O True False

Answer 1

False.

The given signal,
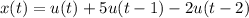`\displaystyle x(t) = u(t) + 5u(t-1) - 2u(t-2)`, is a combination of unit step functions, denoted as
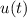`\displaystyle u(t)`. The unit step function is defined as:

`\displaystyle u(t)=\begin{cases}0, & t<0\\ 1, & t\geq 0 \end{cases}`

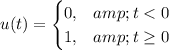
To calculate the average power of a continuous-time signal, we use the formula:

`\displaystyle P_{\text{avg}}=\lim _(T\rightarrow \infty )(1)/(T)\int _{-(T)/(2)}^{(T)/(2)}\left| x(t)\right| ^(2)\, dt`

Applying this formula to the given signal, we have:

`\displaystyle P_{\text{avg}}=\lim _(T\rightarrow \infty )(1)/(T)\int _{-(T)/(2)}^{(T)/(2)}\left| u(t)+5u(t-1)-2u(t-2)\right| ^(2)\, dt`

The signal
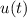`\displaystyle u(t)` is either 0 or 1, so squaring it does not change its value. Therefore, we can simplify the expression:

`\displaystyle P_{\text{avg}}=\lim _(T\rightarrow \infty )(1)/(T)\int _{-(T)/(2)}^{(T)/(2)}\left| 1+5u(t-1)-2u(t-2)\right| ^(2)\, dt`

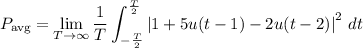
Since the unit step functions only change their values at
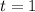`\displaystyle t=1` and
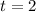`\displaystyle t=2`, the absolute value inside the integral evaluates to:

`\displaystyle \left| 1+5u(t-1)-2u(t-2)\right| =\begin{cases}1, & -(T)/(2)\leq t<0\\6, & 0\leq t<1\\7, & 1\leq t<2\\5, & 2\leq t\leq (T)/(2)\end{cases}`

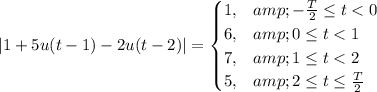
Now, we can split the integral into four intervals based on these values:

`\displaystyle P_{\text{avg}}=\lim _(T\rightarrow \infty )(1)/(T)\left[ \int _{-(T)/(2)}^(0)1^(2)\, dt+\int _(0)^(1)6^(2)\, dt+\int _(1)^(2)7^(2)\, dt+\int _(2)^{(T)/(2)}5^(2)\, dt\right]`

Simplifying each integral, we get:

`\displaystyle P_{\text{avg}}=\lim _(T\rightarrow \infty )(1)/(T)\left[ \left[ t\right] _{-(T)/(2)}^(0)+6^(2)\left[ t\right] _(0)^(1)+7^(2)\left[ t\right] _(1)^(2)+5^(2)\left[ t\right] _(2)^{(T)/(2)}\right]`

`\displaystyle P_{\text{avg}}=\lim _(T\rightarrow \infty )(1)/(T)\left[ 0+6^(2)( 1-0) +7^(2)( 2-1) +5^(2)\left( (T)/(2) -2\right)\right]`

Simplifying further, we have:

`\displaystyle P_{\text{avg}}=\lim _(T\rightarrow \infty )(1)/(T)\left[ 36+49+25\left( (T)/(2) -2\right)\right]`

`\displaystyle P_{\text{avg}}=\lim _(T\rightarrow \infty )(1)/(T)\left( 110+(25T)/(2) -50\right)`

Taking the limit as
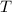`\displaystyle T` approaches infinity, we find:

`\displaystyle P_{\text{avg}}=\lim _(T\rightarrow \infty )(110+(25T)/(2) -50)/(T)`

`\displaystyle P_{\text{avg}}=(25)/(2)`

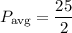
Therefore, the average power of the given signal is
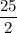`\displaystyle (25)/(2)` Watts, which is not equal to 8W. Hence, the statement is false.

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

♥️
`\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`