a) To rewrite the expression
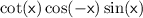 such that the argument
such that the argument
 is positive, we can use the following trigonometric identities:
is positive, we can use the following trigonometric identities:
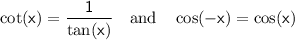 .
.
Applying these identities, we can rewrite the expression as:
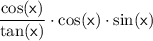 .
.
Simplifying further:
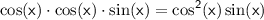 .
.
Therefore, the expression
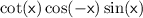 , rewritten such that
, rewritten such that
 is positive, is
is positive, is
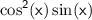 .
.
b) To rewrite the expression
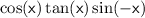 such that
such that
 is positive, we can use the following trigonometric identity:
is positive, we can use the following trigonometric identity:
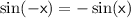 .
.
Applying this identity, we can rewrite the expression as:
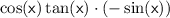 .
.
Simplifying further:
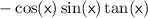 .
.
Therefore, the expression
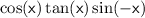 , rewritten such that
, rewritten such that
 is positive, is
is positive, is
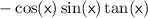 .
.

♥️
