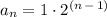Question

Pls help with sequence geometric

Answer 1

`a_n = 2^((n\, -\, 1))`

Explanation:

The general form for a geometric sequence is:

`a_n = a_1 \cdot r^((n\, -\, 1))`

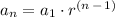
where
`a_n` is the
`n`th term in the sequence,
`a_1` is the 1st term, and
`r` in the common ratio between any two consecutive terms.

In this sequence:

`1, 2, 4, ...`

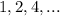
we can identify the common ratio as:

`r= (2)/(1) = (4)/(2) = 2`

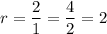
We are also given that the first term is:

`a_1 = 1`

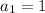
Hence, we can plug these values into the general form for a geometric sequence to get the explicit formula for the given sequence:

`a_n = 1 \cdot 2^((n\, -\, 1))`

`\boxed{a_n = 2^((n\, -\, 1))}`