Question

Many people in the US drink coffee. Suppose the average amount people spend on coffee each month is $73. Suppose that the population standard deviation for the coffee expenditures is known to be $19.50. (a) For a sample of 60 coffee drinkers the standard error is 2.517. (b) For a sample of 40 people the standard error is 3.08. (c) For a sample of 95 people the probability that the sample average will be greater than $67 is: Select ]. (d) For a sample of 95 people the probability that the sample average will be less than $77 is: [Select] (e) For a sample of 95 people the probability that the sample average will be between $72 and $78 is:

Answer 1

(a) For a sample of 60 coffee drinkers the standard error is 2.517.

(b) For a sample of 40 people the standard error is 3.08.

(c) For a sample of 95 people the probability that the sample average will be greater than $67 is: 0.9986 (or 99.86%)

(d) For a sample of 95 people the probability that the sample average will be less than $77 is: 0.9767 (or 97.67%)

(e) For a sample of 95 people the probability that the sample average will be between $72 and $78 is: 0.1256 (or 12.56%)

Explanation:

The standard deviation S = $19.50

The mean u = $73

(a) Sample = n = 60,

then,

`standard \ error = S/√(n) \\standard \ error = 19.50/√(60)\\ standard \ error = 2.517`

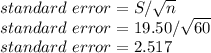
Here, the standard error is 2.517

(b) Sample = n = 40

Standard error = S/sqrt(40)

Standard error = 3.083

(c) Sample = n = 95

Let the sample mean be x,

Probability such that x is greater than $67,

In this case, x = 67

so,

`Z = (x-u)/(S/√(n) )\\Z = (67-73)/(19.50/√(95))\\ Z = -2.9990\\Now, \\P(x > 67) = P(Z > -2.9990)\\P(Z > -2.9990) = 1 - P(Z < -2.9990)\\P(Z > -2.9990) = 1 - 0.0014\\P(Z > -2.9990) = 0.9986`

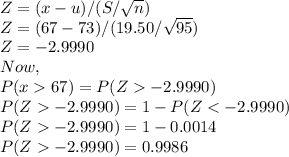
So, the probability that the mean will be greater than $67 is 99.86%

(d) sample = n = 95

let x be sample average

Then, P(x< 77) = ?

Finding Z,

`Z = (x-u)/(S/√(n))\\ Z = (77-73)/(19.50/√(95))\\Z = 1.9993`

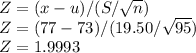
Now,

P(x< 77) = P (Z<1.9993)

Hence P(x<77) = 0.9767

The probability that the mean will be less than $77 is 97.67%

(e) sample = n = 95

We calculate the probabilities that,

P(x>72), and P(x<78)

then, P(72<x<78) = P(x<78) - P(x>72)

Now,

P(x>72)

Finding Z

we get,

`Z = (x-u)/(S/√(n))\\Z = (72-73)/(19.50)/√(95) )\\Z = -0.4998\\`

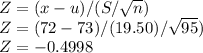
Now,

P(x>72)=P(Z>-0.4998)

P(Z>-0.4998) = 1 - P(z<-0.4998)

which gives,

P(Z>-0.4998) = 1 - 0.312

P(Z>-0.4998) = 0.868

Hence the probability that the mean is greater than $72 is 86.8%

P(x<78)

Finding Z,

`Z = (x-u)/(S/√(n))\\Z = (78-73)/(19.50)/√(95) )\\Z = 2.4992\\`

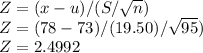
And,we get,

P(Z<2.4992) = 0.9936

Hence, probability that the mean is less than $78 is 99.36%

Finding,P(72<x<78) = P(x<78) - P(x>72)

we get,

P(72<x<78) = 0.9936 - 0.868 = 0.1256

Hence the probability that the sample average will be between $72 and $78 is: 12.56%