Question

(c) The solid is above the cone \( z=\sqrt{x^{2}+y^{2}} \) and lies between the spheres \( x^{2}+y^{2}+z^{2}=4 \) and \( x^{2}+y^{2}+z^{2}=9 \)

Answer 1

The region described is a solid bounded by the cone
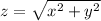`\( z=\sqrt{x^(2)+y^(2)} \)` from below and the spheres
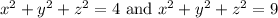`\( x^(2)+y^(2)+z^(2)=4 \) and \( x^(2)+y^(2)+z^(2)=9 \)` from above.

Step-by-step explanation:

To understand this solid, let's break down the given information. The cone
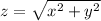`\( z=\sqrt{x^(2)+y^(2)} \)` represents a cone extending infinitely upwards from the xy-plane. The two spheres,
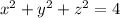`\( x^(2)+y^(2)+z^(2)=4 \)` and
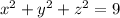`\( x^(2)+y^(2)+z^(2)=9 \)`, denote spheres with radii 2 and 3, respectively, centered at the origin.

Now, considering the constraints provided, the solid is above the cone, meaning it exists in the region where
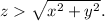`\( z > \sqrt{x^(2)+y^(2)} \).`Additionally, it lies between the spheres, indicating that the solid occupies the space between the two spheres.

In mathematical terms, the solid is defined by the inequalities
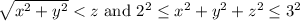`\( \sqrt{x^(2)+y^(2)} < z \) and \( 2^(2) \leq x^(2)+y^(2)+z^(2) \leq 3^(2) \)`. These conditions ensure that the solid is both above the cone and confined within the space between the spheres. This geometric configuration creates a unique region in three-dimensional space that satisfies all given constraints.