Question

Consider the equation:

(2x + 3 / x - 3) + (x + 6 / x - 4) = (x + 6 / x - 3) Add together the numbers of the true statements: 2: -1 is a solution; 4: 4 is in the domain of the variable; 8: The lowest common denominator is (x-3)(x-4); 16: -3 is in the domain of the variable

Answer 1

x = -1

Lowest common denominator is (x-3)(x-4)

Domain is
`(-\infty,3)\cup(3,4)\cup(4,\infty)`

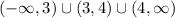
Explanation:

`\displaystyle (2x+3)/(x-3)+(x+6)/(x-4)=(x+6)/(x-3)\\\\((2x+3)(x-4))/((x-3)(x-4))+((x-3)(x+6))/((x-3)(x-4))=((x+6)(x-4))/((x-3)(x-4))\\\\(2x+3)(x-4)+(x-3)(x+6)=(x+6)(x-4)\\\\2x^2-5x-12+x^2+3x-18=x^2+2x-24\\\\3x^2-2x-30=x^2+2x-24\\\\2x^2-2x-30=2x-24\\\\2x^2-4x-30=-24\\\\2x^2-4x-6=0\\\\(2x+2)(x-3)=0\\\\2x+2=0\\2x=-2\\x=-1\\\\x-3=0\\x=3`

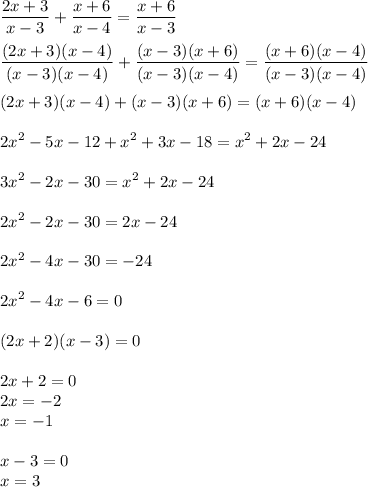
We have to be careful though and reject the solution
`x=3` because plugging it into the original equation makes the denominator 0 on the right and left-hand sides, which is not allowed. Therefore,
`x=-1` is the only solution.

The domain of this function is
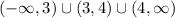`(-\infty,3)\cup(3,4)\cup(4,\infty)` since
`x=3` and
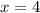`x=4` make the denominators on both sides of the equation 0.