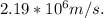Question

One model of the structure of the hydrogen atom consists of a stationary proton with an electron moving in a circular path around it, of radius 5.3 x 10-1 m. The masses of a proton and an electron are 1.673 x 10-27 kg and 9.11 x 10-31 kg, respectively. (a) What is the electrostatic force between the electron and the proton? [] (b) What is the gravitational force between them? [2 ] (c) Which force is mainly responsible for the electron's centripetal motion? [1 ] (d) Calculate the tangential velocity of the electron's orbit around the proton?

Answer 1

The tangential velocity of the electron's orbit around the proton is approximately
`2.19*10^6 m/s.`

Step-by-step explanation:

The tangential velocity of the electron's orbit around the proton can be calculated using the formula for centripetal acceleration.

The centripetal acceleration (a) is given by:

`a = v^2 / r`

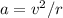
where v is the tangential velocity and r is the radius of the circular path.

In this case, the radius of the circular path is given as
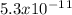`5.3x10^-^1^1` m.

To calculate the tangential velocity (v), we need to find the centripetal acceleration (a) first. The centripetal acceleration can be calculated using the formula:

a = Fc / m

where Fc is the centripetal force and m is the mass of the electron.

In this scenario, the centripetal force is the electrostatic force between the electron and the proton, which we calculated in part (a) to be approximately
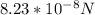`8.23*10^-^8 N`. The mass of the electron is given as
`9.1*10^-^3^1 kg.`

Substituting the values into the equation, we have:

`a = (8.23*10^-^8 N) / (9.1*10^-^3^1 kg)`

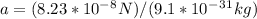
Simplifying the expression, we get:

`a ≈ 9.03*10^2^2 m/s^2`

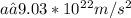
Now, we can calculate the tangential velocity (v) using the formula:

v = √(a * r)

Substituting the values into the equation, we have:

`v = √((9.03*10^2^2 m/s^2) * (5.3*10^-^1^1 m))`

Evaluating the expression, the tangential velocity of the electron's orbit around the proton is approximately
`2.19*10^6 m/s.`