Question

If f(x)=7x+3 ,what is f^-1(x)?

Answer 1

`\displaystyle{f^(-1)(x)=(x)/(7)-(3)/(7)}`

Explanation:

Swap f(x) and x position of the function, thus:

`\displaystyle{x=7f(x)+3}`

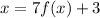
Then solve for f(x), subtract 3 both sides and then divide both by 7:

`\displaystyle{x-3=7f(x)}\\\\\displaystyle{(x)/(7)-(3)/(7)=f(x)}`

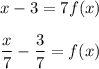
Since the function has been inverted, therefore:

`\displaystyle{f^(-1)(x)=(x)/(7)-(3)/(7)}`

And we can prove the answer by substituting x = 1 in f(x) which results in:

`\displaystyle{f(1)=7(1)+3 = 10}`

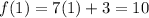
The output is 10, now invert the process by substituting x = 10 in
`f^(-1)(x)`:

`\displaystyle{f^(-1)(10)=(10)/(7)-(3)/(7)}\\\\\displaystyle{f^(-1)(10)=(7)/(7)=1}`

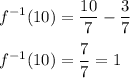
The input is 1. Hence, the solution is true.