In both cases, we have shown that if
 is odd, then
is odd, then
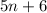 is odd, and if
is odd, and if
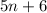 is odd, then
is odd, then
 is odd. This proves that if
is odd. This proves that if
 is a positive integer, then
is a positive integer, then
 is odd if and only if
is odd if and only if
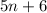 is odd.
is odd.
To prove that if
 is a positive integer, then
is a positive integer, then
 is odd if and only if
is odd if and only if
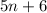 is odd, we need to show both implications separately.
is odd, we need to show both implications separately.
First, let's assume that
 is odd. This means that
is odd. This means that
 can be expressed as
can be expressed as
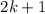 , where
, where
 is an integer.
is an integer.
Now, we can substitute this expression for
 in the equation
in the equation
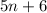 .
.
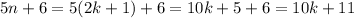
We can rewrite
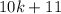 as
as
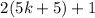 , which is an odd number since
, which is an odd number since
 is an integer.
is an integer.
Therefore, if is odd, then
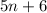 is also odd.
is also odd.
Next, let's assume that
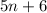 is odd. This means that
is odd. This means that
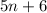 can be expressed as
can be expressed as
 , where
, where
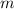 is an integer.
is an integer.
Now, we can solve this equation for
 .
.
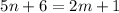
Subtracting 6 from both sides, we have:

Now, we can rewrite
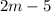 as
as
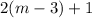 , which is an odd number since
, which is an odd number since
 is an integer.
is an integer.
Therefore, if
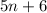 is odd, then
is odd, then
 is also odd.
is also odd.