For Part (a): Eigenvalues and eigenvectors of the matrix representation of T yield the basis B for which the matrix T relative to B is diagonal.
For Part (b): The standard basis
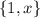 for
for
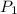 forms the basis B for which the matrix representation of T is already diagonal.
forms the basis B for which the matrix representation of T is already diagonal.
To find a basis B for the domain of T such that the matrix T relative to B is diagonal:
Part (a):
For the linear transformation
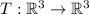 given by
given by
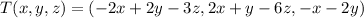 :
:
Approach:
We need to find eigenvectors of T corresponding to distinct eigenvalues. The eigenvectors will form a basis B for which the matrix representation of T will be diagonal.
1. Finding Eigenvalues and Eigenvectors:
- Compute the eigenvalues
 and corresponding eigenvectors v of the matrix representation of T.
and corresponding eigenvectors v of the matrix representation of T.
- Form a basis B using the eigenvectors corresponding to distinct eigenvalues.
Let's proceed with finding the eigenvalues and eigenvectors of T:
The matrix representation of T is:
![\[ [T] = \begin{bmatrix} -2 & 2 & -3 \\ 2 & 1 & -6 \\ -1 & -2 & 0 \end{bmatrix} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/f0hs8m14778eqmbpyegwglglhdclzdkiae.png)
Using this matrix, compute the eigenvalues and eigenvectors.
Part (b):
For the linear transformation
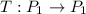 given by
given by
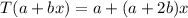 :
:
Approach:
In this case, the space
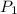 represents polynomials of degree at most 1. The transformation is given by
represents polynomials of degree at most 1. The transformation is given by
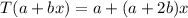 .
.
Since the transformation is defined explicitly, we can find the matrix representation of T directly. A basis B for the domain can be found by considering the standard basis vectors for
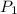 .
.
For , the standard basis is
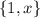 . To check whether the matrix representation of T is diagonalizable or already diagonal, let's represent T in matrix form relative to this basis.
. To check whether the matrix representation of T is diagonalizable or already diagonal, let's represent T in matrix form relative to this basis.
![\[ T(1) = 1 + 0 \cdot x \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ur38l8j9wjia68o9wyhmuu8ltn7xk8en83.png)
![\[ T(x) = 0 + 1 \cdot x \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/yryvcqs6oiov8cr99azda72vmukssk8v4n.png)
The matrix representation of T relative to the basis
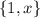 is:
is:
![\[ [T]_B = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/18carpcoezf1kw8k8q8yzlutcmu0echvta.png)
This matrix is already diagonal, and the basis
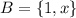 forms the required basis for which the matrix representation of T is diagonal.
forms the required basis for which the matrix representation of T is diagonal.