Question

The midpoint of AB is M(-1,0). If the coordinates of A are (6,-4), what are the coordinates of B?

Answer 1

B(-8, 4)

Explanation:

To find the coordinates of B, use the midpoint formula.

`\boxed{\begin{minipage}{7.4 cm}\underline{Midpoint between two points}\\\\$M=\left((x_2+x_1)/(2),(y_2+y_1)/(2)\right)$\\\\\\where:\\\phantom{ww}$\bullet$ $M$ is the midpoint.\\\phantom{ww}$\bullet$ $(x_1,y_1)$ and $(x_2,y_2)$ are the endpoints.\\\end{minipage}}`

Let point A be (x₁, y₁). Therefore, (x₁, y₁) = (6, -4).

Let point B be (x₂, y₂).

The midpoint M is (-1, 0).

Substitute these values into the midpoint formula:

`(-1, 0)=\left((x_2+6)/(2),(y_2-4)/(2)\right)`

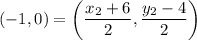
Solve the x and y coordinates separately:

`\begin{aligned}(x_2+6)/(2)&=-1\\\\x_2+6&=-2\\\\x_2&=-8\end{aligned}`
`\begin{aligned}(y_2-4)/(2)&=0\\\\y_2-4&=0\\\\y_2&=4\end{aligned}`

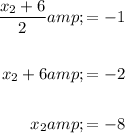
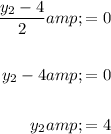
Therefore, the coordinates of point B are (-8, 4).