Question

Find the center of the ellipse defined by the equation... 100 points

Answer 1

(-4,4)

Explanation:

You rewrite the terms:

(x + 4)^2 => [x - (-4)]^2

(y - 4)^2 => [y - (4)]^2

so h = -4 and k = 4

so center of ellipse is (h,k) or (-4,4)

Answer 2

Center = (-4, 4)

Explanation:

The standard form of the equation of an ellipse with center (h, k) is:

`\boxed{((x-h)^2)/(a^2)+((y-k)^2)/(b^2)=1}`

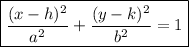
The given equation is:

`((x+4)^2)/(25)+((y-4)^2)/(9)=1`

Comparing the given equation with the standard form, we can see that h = -4 and k = 4. Therefore, the center (h, k) of the ellipse is (-4, 4).