Question

PLEASE HELP AND GIVE ME A STEP BY STEP EXPLAINING I OWE YOU MY LIFE

Answer 1

a) ∠BAD = 67.4

b) ∠BDC = 22.6

c) BC = 4.6

Explanation:

a) tan θ = opposite/adjacent

In Δ ABD,

tan ∠BAD = DB/AD

tan ∠BAD = 12/5

∠BAD = tan⁻¹(12/5)

∠BAD = 67.4

b) In In Δ ABD,

∠BAD + ∠ABD + ∠ADB = 180°

⇒ ∠ABD = 180 - ∠BAD - ∠ADB

= 180 - 67.4 - 90

∠ABD = 22.6

In trapezium, since AB and DC are parallel,

∠BDC = ∠ABD (alternate interior angles)

⇒ ∠BDC = 22.6

c) In In Δ ABD,

AB² = AD² + DB²

= 5² + 12²

= 25 + 144

= 169

= 13²

AB² = 13²

⇒ AB = 13

In Δ ABD and Δ BDC,

∠ADB = ∠BCD

∠ABD = ∠BDC

Since two angles are equal, the thrid angle must also be equal

∠BAD = ∠BDC

∴ Δ ABD and Δ BDC are similar

∴ the ratio of the corresponding sides should be equal

⇒
`(BD)/(AB) = (BC)/(AD)= (DC)/(BD) \\`

`\implies (12)/(13) = (BC)/(5)= (DC)/(12) \\\\\\\implies (12)/(13) = (BC)/(5)\\\\\implies BC = (12*5)/(13)\\\\\implies BC = (60)/(13)`

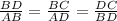
⇒ BC = 4.6