Question

NO LINKS!!! URGENT HELP PLEASE!!!

Please help with 27 & 28
​

Answer 1

27) 34.29 in²

28) If I get an A, then I studied for my final.

Explanation:

Question 27

To calculate the area of the trapezoid, we need to find its perpendicular height.

As the given diagram shows an isosceles trapezoid (since the non-parallel sides (the legs) are of equal length), we can use Pythagoras Theorem to calculate the perpendicular height.

Identify the right triangle formed by drawing the perpendicular height from the vertex of the bottom base to the top base (this has been done for you in the given diagram).

As the two base angles of an isosceles trapezoid are always congruent, the base of the right triangle is half the difference between the lengths of the parallel bases, which is (8 - 6)/2 = 1 inch.

The hypotenuse of the right triangle is the leg of the trapezoid, which is 5 inches.

Use Pythagoras Theorem to find the perpendicular height (the length of the other leg):

`h^2+1^2=5^2`

`h^2+1=25`

`h^2=24`

`h=√(24)`

`h=2√(6)`

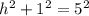
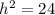
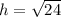
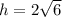
Now we have found the height of the trapezoid, we can use the following formula to calculate its area:

`\boxed{\begin{minipage}{7 cm}\underline{Area of a trapezoid}\\\\$A=(1)/(2)(a+b)h$\\\\where:\\ \phantom{ww}$\bullet$ $A$ is the area.\\ \phantom{ww}$\bullet$ $a$ and $b$ are the parallel sides (bases).\\\phantom{ww}$\bullet$ $h$ is the height.\\\end{minipage}}`

The values to substitute into the area formula are:

• a = 8 in
• b = 6 in
• h = 2√6 in

Substituting these values into the formula we get:

`A=(1)/(2)(8+6) \cdot 2√(6)`

`A=(1)/(2)(14) \cdot 2√(6)`

`A=7\cdot 2√(6)`

`A=14√(6)`

`A=34.29\; \sf in^2\;(nearest\;hundredth)`

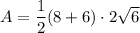
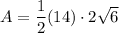
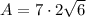
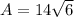
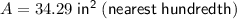
Therefore, the area of the isosceles trapezoid is 34.29 in², rounded to the nearest hundredth.

`\hrulefill`

Question 28

Given conditional statement:

• "If I studied for my final, then I will get an A"

The hypothesis is "I studied for my final", and the conclusion is "I will get an A".

The converse of a conditional statement involves switching the hypothesis ("if" part) and the conclusion ("then" part) of the original statement.

Therefore, the converse of the statement would be:

• "If I get an A, then I studied for my final."