Question

Does the series converge or diverge? if it converges, what is the sum? SHOW YOUR WORK!!!!!!

equation is in picture.

Answer 1

Yes the partial sums should get closer to -3.

Answer 2

Answer: It converges to -3

=============================================

Reason:

This is a geometric series with

• a = -4 = first term
• r = -1/3 = common ratio

The template is
`a(r)^(n-1)`

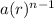
If -1 < r < 1, then the infinite geometric series converges to a finite number. This is because we add on smaller and smaller pieces, which prevents the sum going off to infinity.

In the case of r = -1/3, it fits the interval -1 < r < 1. In other words -1 < -1/3 < 1 is true.

We'll plug those values into the formula below to wrap things up.

`S = (a)/(1-r)\\\\S = (-4)/(1-(-1/3))\\\\S = (-4)/(1+1/3)\\\\S = (-4)/(3/3+1/3)\\\\`

`S = (-4)/(4/3)\\\\S = -4 / (4)/(3)\\\\S = (-4)/(1) * (3)/(4)\\\\S = (-4*3)/(1*4)\\\\S = -3\\\\`

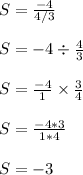
Therefore,

`\displaystyle \sum_(n=1)^(\infty) -4\left(-(1)/(3)\right)^(n-1) = -3`

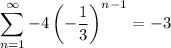
The final answer is -3.

You can verify the answer by generating partial sums with a spreadsheet. The partial sums should steadily get closer to -3.

Here's a few partial sums.

`\begin{array}c \cline{1-3}\text{n} & \text{a}_{\text{n}} & \text{S}_{\text{n}}\\\cline{1-3}1 & -4 & -4\\\cline{1-3}2 & 1.333333 & -2.666667\\\cline{1-3}3 & -0.444444 & -3.111111\\\cline{1-3}4 & 0.148148 & -2.962963\\\cline{1-3}5 & -0.049383 & -3.012346\\\cline{1-3}6 & 0.016461 & -2.995885\\\cline{1-3}7 & -0.005487 & -3.001372\\\cline{1-3}8 & 0.001829 & -2.999543\\\cline{1-3}9 & -0.00061 & -3.000153\\\cline{1-3}10 & 0.000203 & -2.99995\\\cline{1-3}\end{array}`

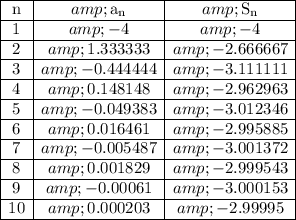
The interesting thing is that the partial sums
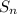`S_n` bounce around -3 while also getting closer to it.