Answer:
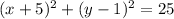
Explanation:
To determine the equation of the graphed circle, we need to find the coordinates of its center and the length of its radius.
The center of the circle is a single point that lies at an equal distance from all points on the circumference of the circle.
From inspection of the graphed circle, we can see that its domain is [-10, 0] and its range is [-4, 6]. The x-coordinate of the center is the midpoint of the domain, and the y-coordinate of the center is the midpoint of the range.
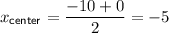
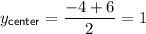
Therefore, the center of the circle is (-5, 1).
The radius of the circle is the distance from the center to all points on the circumference of the circle. Therefore, to calculate the length of the radius, find the distance between x-coordinate of the center and one of the endpoints of the domain.
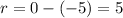
Therefore, the radius of the circle is r = 5.
To determine the equation of the circle, substitute the center and radius into the standard formula.

As h = -5, k = 1 and r = 5, then:
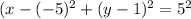
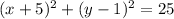
Therefore, the equation of the graphed circle is:
