Question

What is the value of P in the triangle below?

Answer 1

8√3

Explanation:

pythagoras theorem

16^2=8^2+p^2

p= √(16^2-8^2)

= 8√3

Answer 2

P = 8√3

Explanation:

Apply the Pythagoras Theorem:

`\displaystyle{\text{opposite}^2+\text{adjacent}^2=\text{hypotenuse}^2}`

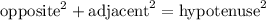
Commonly written as:

`\displaystyle{a^2+b^2=c^2}`

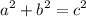
From the attachment, we know that opposite = 8 and hypotenuse = 18. Solve for the adjacent (P). Therefore:

`\displaystyle{8^2+P^2=16^2}\\\\\displaystyle{64+P^2=16^2}`

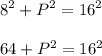
Subtract 64 both sides to isolate P:

`\displaystyle{P^2=16^2-64}\\\\\displaystyle{P^2=256-64}\\\\\displaystyle{P^2=192}`

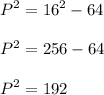
Square root both sides:

`\displaystyle{√(P^2) = √(192)}\\\\\displaystyle{P=√(192)}`

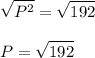
192 can be factored as 8 x 8 x 3. Therefore:

`\displaystyle{P=√(8 * 8 * 3)}\\\\\displaystyle{P = 8√(3)}`

Thus, P = 8√3