Question

NO LINKS!! URGENT HELP PLEASE!!​

Answer 1

7a) QS = 16 units

7b) 96 square units

8) 30 units

Explanation:

Question 7a

The sides lengths of a rhombus are equal.

Therefore, if the rhombus has a perimeter of 40, each side length is 10, since 40 ÷ 4 = 10.

PQ = QR = RS = SP = 10

The diagonals of a rhombus are perpendicular bisectors of each other.

Therefore, if PR is 12, then PM = 6.

Also, if QM + MS = QS, and QM = MS, then QS = 2·QM.

As the diagonals bisect each other at right angles, triangle PMQ is a right triangle, where:

• PM = 6
• PQ = 10
• m∠PMQ = 90°

Using Pythagoras Theorem to find the length of QM:

`PM^2+QM^2=PQ^2`

`6^2+QM^2=10^2`

`36+QM^2=100`

`QM^2=64`

`QM=8`

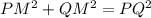
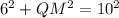
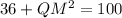
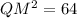
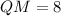
As QS = 2·QM, then:

`QS = 2 \cdot 8`

`QS = 16`

`\hrulefill`

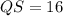
Question 7b

The formula for the area of a rhombus is half the product of its diagonals.

`\boxed{\begin{minipage}{5 cm}\underline{Area of a rhombus} \\\\$A=(1)/(2)pq$\\\\where:\\ \phantom{ww}$\bullet$ $p$ and $q$ are the diagonals.\\\end{minipage}}`

Therefore, given the diagonals of the rhombus are PR = 12 and QS = 16, the area of the rhombus is:

`\begin{aligned}\textsf{Area}&=(1)/(2) \cdot 12 \cdot 16\\\\&=6 \cdot 16\\\\&=96\; \sf square\;units\end{aligned}`

`\hrulefill`

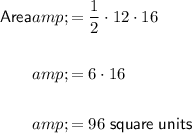
Question 8

The formula for the perimeter of a rhombus given its diagonals is:

`\boxed{\begin{minipage}{5 cm}\underline{Perimeter of a rhombus} \\\\$P=2√(p^2+q^2)$\\\\where:\\ \phantom{ww}$\bullet$ $p$ and $q$ are the diagonals.\\\end{minipage}}`

If the diagonals are 9 and 12, the perimeter is:

`\begin{aligned}\textsf{Perimeter}&=2√(9^2+12^2)\\&=2√(81+144)\\&=2√(225)\\&=2 \cdot 15\\&=30\end{aligned}`

Therefore, the perimeter of the rhombus is 30 units.

Answer 2

7. a. 16 units b. 96 square units.

8. 30 units

Explanation:

7.

a. The perimeter of a rhombus is 40, and PR is 12.

This means that all four sides are equal, and each side is 10.

Since diagonal bisect each other creating right angle.

so

In ΔPMS

PS=10

PM=1/2 of PR= 1/2*12=6

Now by using Pythagoras theorem:

PS²=MS²+PM²

10²=MS²+6²

MS²=100-36

MS²=64

MS=
`√(64)=8`

Therefore, diagonal QS=2*MS=2*8=16 units

b.

Since the area of a rhombus is half the product of its diagonals. The diagonals of this rhombus are QS=16 and PR=12,

So, Area=1/2*PR*QS

=1/2*12*16

=96 square units.

8.

The perimeter of a rhombus is the total length of all four sides.

Since the diagonals of a rhombus bisect each other at right angles, we can use the Pythagorean Theorem to find the length of one side of the rhombus.

let d1=9 and d2=12

`s = √((d1/2)^2 + (d2/2)^2)`

`s = √((9/2)^2 + (12/2)^2)`

s=7.5

we have

P = 4s where p is perimeter

P=4*7.5

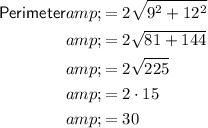
Therefore, the perimeter of the rhombus is 30 units.