Question

An important property of logarithms is: a) \( \log _{a} a=a \) b) \( \log _{a} a=1 \) c) \( \log _{1} a=a \) d) \( \log _{1} 1=1 \)

Answer 1

(b)
`\log _(a) a=1`

Explanation:

You want to know which equation represents an important property of logarithms.

`\text{a) } (\log _(a) a=a)\\\text{b) }(\log _(a) a=1) \\\text{c) }( \log _(1) a=a\\ \text{d) }(\log _(1) 1=1)`

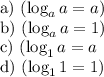
Logarithm

A logarithm is the exponent of the base that results in its argument:

`\log_b(a)=x\quad\leftrightarrow\quad a=b^x`

This lets us sort through the choices:

a) a^a ≠ a

b) a^1 = a . . . . true

c) 1^a ≠ a

d) 1^1 = 1 . . . . not generally a property of logarithms (see comment)

The correct choice is ...

`\boxed{\log _(a) a=1}`

__

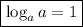
Additional comment

A logarithm to the base 1 is generally considered to be undefined. That is because the "change of base formula" tells us ...

`\log_b(a)=(\log(a))/(\log(b))`

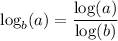
The log of 1 is 0, so this ratio is undefined for b=1.

<95141404393>