Question

Find the length of the curve.
y=∫[1, x] (((t^3)-1)^(1/2))dt (1<=x<=11)

Answer 1

160.125

Explanation:

Recall that the length of a curve is
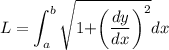`\displaystyle L=\int^b_a\sqrt{1+\biggr((dy)/(dx)\biggr)^2}dx`, so we'll need to determine
`(dy)/(dx)` using Fundamental Theorem of Calculus Part 1:

`\displaystyle y=\int^x_1√(t^3-1)\,dt\\\\(dy)/(dx)=(d)/(dx)\int^x_1√(t^3-1)\,dt\\\\(dy)/(dx)=√(x^3-1)`

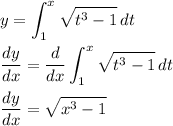
Now that we've done so, we can plug
`(dy)/(dx)` into our formula from before and get the length of the parametric curve:

`\displaystyle L=\int^b_a\sqrt{1+\biggr((dy)/(dx)\biggr)^2}\,dx\\\\L=\int^(11)_1\sqrt{1+√(x^3-1)^2}\,dx\\\\L=\int^(11)_1√(1+x^3-1)\,dx\\\\L=\int^(11)_1√(x^3)\,dx\\\\L=\int^(11)_1x^(3)/(2)\,dx\\\\L=(2)/(5)x^(5)/(2)\biggr|^(11)_1\\\\L=(2)/(5)(11)^(5)/(2)-(2)/(5)(1)^(5)/(2)\\\\L\approx160.125`

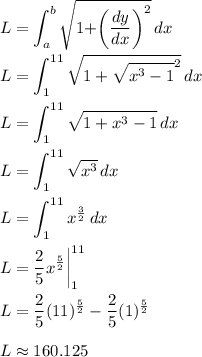
Therefore, the length of the curve is about 160.125 units.