Answer: HK is about 14.2 yards.
Step-by-step explanation: To find HK, we need to use the triangle angle sum theorem, which states that the sum of all the interior angles of a triangle is 180 degrees. We can use this theorem to find the missing angle in triangle HJK.
We know that m<H = 40° and m<K = 50°. So, m<J = 180° - (40° + 50°) = 90°. This means that triangle HJK is a right triangle, and we can use the Pythagorean theorem to find HK.
The Pythagorean theorem states that for any right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. In this case, HK is the hypotenuse, and JK and HJ are the other two sides. So, we have:
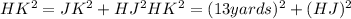
To find HJ, we need to use trigonometry. We can use the tangent ratio, which relates an acute angle in a right triangle to the opposite side and the adjacent side. In this case, we can use angle H:
tan(H) = opposite/adjacent tan(40°) = HJ/JK HJ = tan(40°) * JK HJ = tan(40°) * 13 yards HJ ≈ 11 yards
Now, we can plug this value into the Pythagorean theorem and solve for HK:
HK^2 = (13 yards)^2 + (11 yards)^2 HK^2 = 169 yards^2 + 121 yards^2 HK^2 = 290 yards^2 HK = √290 yards HK ≈ 14.2 yards
Therefore, HK is about 14.2 yards long. Hope this helps! =)