Question

Evaluate the integral
14. \( \int \frac{d t}{t^{2} \sqrt{t^{2}-16}} \)

Answer 1

To evaluate the integral, we can use a substitution. Let's substitute
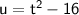`\sf u = t^2 - 16`. Then,
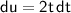`\sf du = 2t \, dt`. Rearranging this equation, we have
`\sf dt = (du)/(2t)`.

Substituting
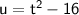`\sf u = t^2 - 16` and
`\sf dt = (du)/(2t)` into the integral, we get:

`\sf \int (dt)/(t^2 √(t^2 - 16)) = \int ((du)/(2t))/(t^2 √(u)) = (1)/(2) \int (du)/(t^3 √(u))`

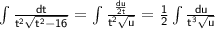
Now, we can simplify the integral to have only one variable. Recall that
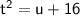`\sf t^2 = u + 16`. Substituting this into the integral, we have:

`\sf (1)/(2) \int (du)/((u+16) √(u))`

To simplify further, we can split the fraction into two separate fractions:

`\sf (1)/(2) \left( \int (du)/((u+16) √(u)) \right) = (1)/(2) \left( \int (du)/(u √(u)) + \int (du)/(16 √(u)) \right)`

Now, we can integrate each term separately:

`\sf (1)/(2) \left( \int u^{-(3)/(2)} \, du + \int 16^{-(1)/(2)} \, du \right) = (1)/(2) \left( -2u^{-(1)/(2)} + 4 √(u) \right) + C`

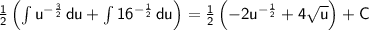
Finally, we substitute back
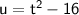`\sf u = t^2 - 16` and simplify:

`\sf (1)/(2) \left( -2(t^2 - 16)^{-(1)/(2)} + 4 √(t^2 - 16) \right) + C`

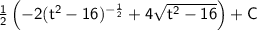
Therefore, the evaluated integral is
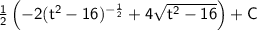`\sf (1)/(2) \left( -2(t^2 - 16)^{-(1)/(2)} + 4 √(t^2 - 16) \right) + C`.

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

♥️
`\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`