Answer:
y = 2x - 4
Explanation:
To solve this problem, we must first calculate the slope of the line AB using the formula:
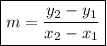
where:
m ⇒ slope of the line
(x₁, y₁), (x₂, y₂) ⇒ coordinates of two points on the line
Therefore, for line AB with points A = (2, 5) and B = (4, 4) :
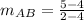
⇒

⇒
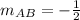
Next, we have to calculate the slope of the line BC.
We know that the product of the slopes of two perpendicular lines is -1.
Therefore:
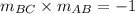 [Since BC and AB are at right angles to each other]
[Since BC and AB are at right angles to each other]
⇒
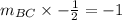
⇒
 [Dividing both sides of the equation by -1/2]
[Dividing both sides of the equation by -1/2]
⇒

Next, we have to use the following formula to find the equation of line BC:

where (x₁, y₁) are the coordinates of a point on the line.
Point B = (4, 4) is on line BC, and its slope is 2. Therefore:
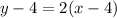
⇒
 [Distributing 2 into the brackets]
[Distributing 2 into the brackets]
⇒
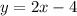
Therefore, the equation of line BC is y = 2x - 4.