To evaluate the limit
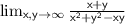 , we can analyze the behavior of the expression as both
, we can analyze the behavior of the expression as both
 and
and
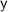 approach infinity.
approach infinity.
Let's consider the numerator
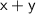 and the denominator
and the denominator
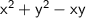 separately.
separately.
For the numerator, as both
 and
and
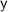 approach infinity, their sum
approach infinity, their sum
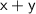 will also approach infinity.
will also approach infinity.
For the denominator, we can rewrite it as
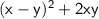 . As
. As
 and
and
 approach infinity, the terms
approach infinity, the terms
 and
and
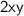 will also approach infinity. Therefore, the denominator will also approach infinity.
will also approach infinity. Therefore, the denominator will also approach infinity.
Now, let's consider the entire fraction
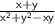 . Since both the numerator and denominator approach infinity, we have an indeterminate form of
. Since both the numerator and denominator approach infinity, we have an indeterminate form of
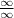 .
.
To evaluate this indeterminate form, we can apply techniques such as L'Hôpital's rule or algebraic manipulations. However, in this case, we can simplify the expression further.
By dividing both the numerator and denominator by
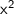 , we get:
, we get:
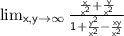
As
 approaches infinity, the terms
approaches infinity, the terms
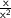 and
and
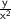 both approach zero. Similarly, the term
both approach zero. Similarly, the term
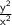 and
and
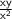 also approach zero.
also approach zero.
Therefore, the limit simplifies to:

Hence, the limit
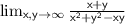 is equal to 0.
is equal to 0.