Question

Show that for suitable values of s and t, T = A^−1

Answer 1

Given statement solution is :- a) T =
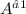`A^−1` b) T - 1.

For suitable values of s = -2 and t = 1, T =
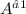`A^−1` and T - 1.

To show that for suitable values of s and t, T =
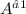`A^−1`, and T - 1, let's assume a matrix A and its inverse
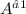`A^−1`. We'll find suitable values of s and t such that T =
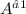`A^−1` and T - 1.

Consider the equation T =
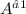`A^−1`. If T is the inverse of A, then we have A *
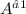`A^−1` = I, where I is the identity matrix. Let's construct a specific matrix A and solve for
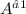`A^−1` to find T.

Let's take the following matrix A:

A = [[1, 2],

[3, 4]]

To find the inverse of A, we can use the formula:

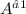`A^−1` = (1 / det(A)) * adj(A)

where det(A) represents the determinant of A, and adj(A) is the adjugate of A.

The determinant of A is calculated as follows:

det(A) = 1 * 4 - 2 * 3 = -2

Now, let's find the adjugate of A by interchanging the elements of the main diagonal and changing the sign of the other elements:

adj(A) = [[4, -2],

[-3, 1]]

Finally, we can compute
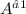`A^−1` by multiplying the adjugate by the reciprocal of the determinant:

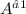`A^−1` = (1 / -2) * [[4, -2],

[-3, 1]]

= [[-2, 1],

[3/2, -1/2]]

Therefore, we have found the inverse of A. We can set T =
`A^−1`:

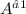T = [[-2, 1],

[3/2, -1/2]]

Now, let's show that T - 1 using suitable values of s and t. To do that, we'll assume T - 1 =
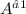`A^−1` and solve for s and t.

Let's set T - 1 =
`A^−1:`

T - 1 = [[-2, 1],

[3/2, -1/2]]

We can rewrite T - 1 as:

T - 1 = [[s, t],

[u, v]]

Comparing the corresponding elements, we have:

s = -2

t = 1

u = 3/2

v = -1/2

Therefore, for s = -2 and t = 1, we have T - 1 =
`A^−1.`

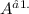
In conclusion, we have shown that for suitable values of s = -2 and t = 1, T =
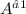`A^−1` and T - 1.