Question

A population is normally distributed with a mean of $63,015 and a standard deviation of $11,467. Determine the value such that 99% of all other values are smaller than this one.

Answer 1

To determine the value such that 99% of all other values are smaller, we can use the concept of the standard normal distribution and the z-score.

Given a normally distributed population with a mean
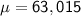`\sf \mu = 63,015 \\` and a standard deviation
`\sf \sigma = 11,467 \\`, we want to find the value
`\sf x \\` such that 99% of the values are smaller than
`\sf x \\`.

To do this, we need to find the z-score corresponding to the desired percentile (in this case, 99%). We can use a standard normal distribution table or a calculator to find the z-score.

Using a standard normal distribution table, we find that the z-score corresponding to the 99th percentile is approximately 2.326.

The z-score formula is given by:

`\sf z = (x - \mu)/(\sigma) \\`

Rearranging the formula to solve for
`\sf x \\`:

`\sf x = z \cdot \sigma + \mu \\`

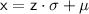
Substituting the known values:

`\sf x = 2.326 \cdot 11,467 + 63,015 \\`

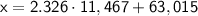
Calculating:

`\sf x \approx 26,693.46 + 63,015 \\`

`\sf x \approx 89,708.46 \\`

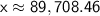
Therefore, the value such that 99% of all other values are smaller is approximately $89,708.46.