Question

QUESTION IS IN THE PICTURE.

Answer 1

`\displaystyle{=-(p^5)/(6)}`

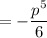
Explanation:

Given the expression:

`\displaystyle{(1)/(-6p^(-5))}`

We have to apply the negative exponent law where:

`\displaystyle{x^(-n) =(1)/(x^n)}`

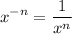
Thus:

`\displaystyle{(1)/(-6p^(-5))= (1)/(-6\cdot (1)/(p^5))}\\\\\displaystyle{=(1)/( - (6)/(p^5) )}\\\\\displaystyle{= 1 \cdot \left(-(p^5)/(6)\right)}\\\\\displaystyle{=-(p^5)/(6)}`

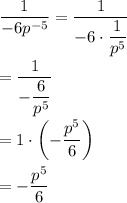
But there's a trick here, consider this:

`\displaystyle{(a)/(kb^(-n))}\\\\\displaystyle{=(a)/((k)/(b^n))}\\\\\displaystyle{=(ab^n)/(k)}`

So the trick is to just move
`p^(-5)` up then you'll have
`p^5` as a numerator (top) which still results the same as the answer.