Question

For the function f(x) = 3 logx, estimate ƒ' (1) using a positive difference quotient. From the graph of f(x), would you expect you

estimate to be greater than or less than f' (1)?
Round your answer to three decimal places.
f' (1) =

Answer 1

To estimate
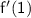`\sf f'(1) \\` using a positive difference quotient for the function
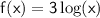`\sf f(x) = 3\log(x) \\`, we can use the following formula:

`\sf f'(1) \approx (f(1+h) - f(1))/(h)\\`

where
`\sf h \\` is a small positive value. Let's choose
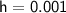`\sf h = 0.001 \\` for our estimation.

First, let's evaluate
`\sf f(1) \\`:

`\sf f(1) = 3\log(1) = 3\cdot 0 = 0 \\`

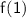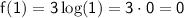
Next, let's evaluate
`\sf f(1+h) \\`:

`\sf f(1+h) = 3\log(1+h) \\`

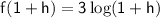
Substituting
`\sf h = 0.001 \\`:

`\sf f(1+0.001) = 3\log(1.001) \\`

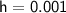Now, we can calculate the positive difference quotient:

`\sf f'(1) \approx (f(1+h) - f(1))/(h) = (3\log(1.001) - 0)/(0.001) \\`

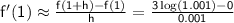
Using a calculator, we find:

`\sf f'(1) \approx 0.434 \\`

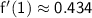
Therefore,
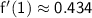`\sf f'(1) \approx 0.434 \\` (rounded to three decimal places).

From the graph of
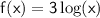`\sf f(x) = 3\log(x) \\`, we would expect the estimate
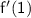`\sf f'(1) \\` to be greater than
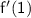`\sf f'(1) \\` since the graph of
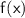`\sf f(x) \\` is increasing at
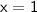`\sf x = 1 \\`.