Question

Nicole invests $2000 in an account. The account pays compound interest at a rate of K% per year. At the end of the first year, the money in the account is $2036. (i) Show that K = 1.8. (ii) Find the number of complete years before Nicole has at least $2150 in the account. Show full working​

Answer 1

(i) K = 1.8 (Given in explanation)

(ii) Nicole will have the required amount of $2150 after 5 complete years

Explanation:

The formula for compound interest is,

`A = P(1+r/n)^(nt)`

Where A is the final amount

P is the initial amount

r is the interest rate

n is the number of times the interest is applied per time period

t is the number of time periods elapsed

(i) In our case,

P = initial amount = $2000

A = final amount = #2036

r = K%

n = 1 (The account pays compound interest once per year and the time period is in years)

And for the 1st case, t = 1 year

so,

`A = P(1+r/n)^(nt)\\2036 = 2000(1+K/100)^(1)`

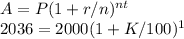
Note: 1/100 = 1% so K/100 = K%

`2036/2000 = (1+K/100)\\2036/2000 - 1 =K/100\\1.018 -1 = K/100\\0.018=K/100\\K=(100)(0.018)\\\\K=1.8`

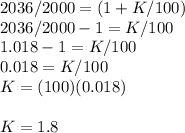
Hence shown that K = 1.8

(ii)For the 2nd case, A = $2150 but in this case, we need to find the number of years t and we have found K from the previous problem K = 1.8

So,

`2150 = 2000(1+1.8/100)^(t)\\2150/2000 = (1+1.8/100)^(t)\\1.075 = (1+1.8/100)^(t)\\`

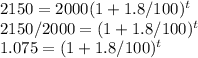
Now, we take the log on both sides,

`log(1.075) = log(1 + 1.8/100)^t`

Using the property,

`log(A)^B = (B)(log(A)`

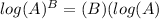
we get,

`log(1.075) = (t)log(1 + 1.8/100)\\log(1.075) = (t)log(1.018)\\log(1.075)/log(1.018) = t\\Which \ gives,\\t = 4.054 \ years`

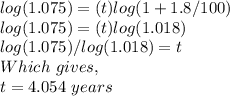
So, after 4 years, Nicole will have less than $2150 since it requires 4.054 years,

Hence, Nicole will have the required amount of $2150 after 5 complete years