Answer:
Approximately
 .
.
(Assumptions:
 ; air resistance on the volleyball is negligible.)
; air resistance on the volleyball is negligible.)
Step-by-step explanation:
Under the assumptions, acceleration of the volleyball would be
 during the entire flight. (This value is negative since the ball is accelerating downwards- toward the ground.)
during the entire flight. (This value is negative since the ball is accelerating downwards- toward the ground.)
By the time the volleyball hits the ground, the volleyball would be at a position
 below where it was launched. In other words, the (vertical) displacement of the volleyball during the entire flight would be
below where it was launched. In other words, the (vertical) displacement of the volleyball during the entire flight would be
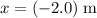 . (Negative since the ball is below where it was launched.)
. (Negative since the ball is below where it was launched.)
Apply the SUVAT equation
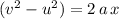 to find the velocity of the volleyball right before hitting the ground. In this equation:
to find the velocity of the volleyball right before hitting the ground. In this equation:
 is the velocity of the volleyball right before hitting the ground,
is the velocity of the volleyball right before hitting the ground,
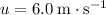 is the initial velocity of the volleyball,
is the initial velocity of the volleyball,
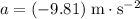 is the acceleration of the volleyball, and
is the acceleration of the volleyball, and
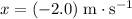 is the displacement of the volleyball during the flight.
is the displacement of the volleyball during the flight.
Rearrange this equation and solve for the velocity right before landing,
 . Note that because
. Note that because
 is raised to the power of
is raised to the power of
 in
in
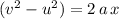 , both
, both
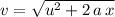 and
and
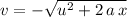 could satisfy this equation. However,
could satisfy this equation. However,
 needs to be negative since the volleyball would be travelling downwards before reaching the ground.
needs to be negative since the volleyball would be travelling downwards before reaching the ground.
Therefore, right before reaching the ground, velocity of the volleyball would be:
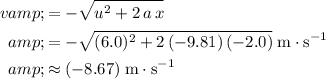 .
.
In other words, velocity of this volleyball has changed from
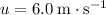 (upwards) to
(upwards) to
 (downwards) during this flight. Divide the change in the velocity
(downwards) during this flight. Divide the change in the velocity
 by the rate of change in velocity
by the rate of change in velocity
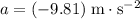 to find the duration of this flight:
to find the duration of this flight:
 .
.