Question

20 The centre of a circle is the point with coordinates (-1,3) The point A with coordinates (6, 8) lies on the circle. Find an equation of the tangent to the circle at A. Give your answer in the form ax + by+c=0 where a, b and c are integers.​

Answer 1

Explanation:

Start by writing the formula for the circle

`(x+1)^2+(y-3)^2=r^2`

find the radius by using the distance formula

`r=√((6+1)^2+(3-8)^2)=8.60232526704\\(x+1)^2+(y-3)^2=8.60232526704^2`

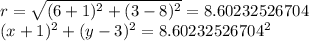
To find a and b take the derivative and plug in the x and y coordinate

`a=(d)/(dx)((x+1)^2+(y-3)^2)= 2(x+1) = 2*(6+1)=14\\b=(d)/(dy)((x+1)^2+(y-3)^2)=2(y-3)=2*(8-3)=10\\`

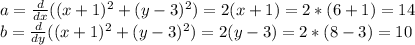
now we just need c. because the line must pass through (6,8) we can plug in a and b and solve for c

`14*6+10*8+c=0\\c= -164`

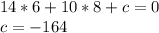
Thus, the final answer is

14x+10y-164=0