Question

Part of a cross-country skier's path can be described with the vector function r = <2 + 6t + 2 cos(t), (15 − t)(1 − sin(t))> for 0 ≤ t ≤ 15 minutes, with x and y measured in meters. The derivatives of these functions are given by x′(t) = 6 − 2sin(t) and y′(t) = −15cos(t) + tcos(t) − 1 + sin(t). 1. Find the slope of the path at time t = 4. Show the computations that lead to your answer. 2. Find the time when the skier's horizontal position is x = 60. 3. Find the acceleration vector of the skier when the skier's horizontal position is x = 60. 4. Find the speed of the skier when he is at his maximum height and find his speed in meters/min. 5. Find the total distance in meters that the skier travels from t = 0 to t = 15 minutes

Answer 1

1. The slope of the path at time t = 4 The function of the path of the cross-country skier is given by
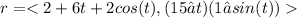`r = < 2 + 6t + 2 cos(t), (15 − t)(1 − sin(t)) >` for
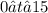`0 ≤ t ≤ 15` minutes The derivatives of the x and y functions are

`x′(t) = 6 − 2sin(t) and y′(t) = −15cos(t) + tcos(t) − 1 + sin(t).`

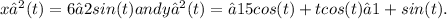
The slope of the path at time t = 4 can be determined by the derivative of the function with respect to t. The derivative of the function is given by:

`r' = < 6 − 2sin(t), −15cos(t) + tcos(t) − 1 + sin(t) >`

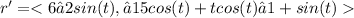
Let's calculate the slope of the path at t = 4:

`r'(4) = < 6 − 2sin(4), −15cos(4) + 4cos(4) − 1 + sin(4) > = < 3.75, -15.12 >`

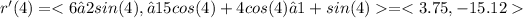
The slope of the path at time t = 4 is 3.75.

2. The time when the skier's horizontal position is x = 60.

The x-component of the vector function is given by
`x = 2 + 6t + 2cos(t)`

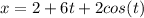
3. To find the time when the skier's horizontal position is x = 60, let's solve for t as follows:
`2 + 6t + 2cos(t) = 60 ⇒ 6t + 2cos(t) \\= 58 ⇒ 3t + cos(t) \\= 29t ≈ 4.056 minutes3.`

The acceleration vector of the skier when the skier's horizontal position is x = 60.

The horizontal position of the skier is given by
`x = 2 + 6t + 2cos(t)`

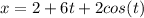
Differentiating the equation twice with respect to t will give the acceleration vector of the skier.

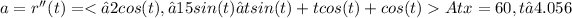`a = r''(t) = < −2cos(t), −15sin(t) − t sin(t) + tcos(t) + cos(t) > At x = 60, t ≈ 4.056`minutes, the acceleration vector is:

`a ≈ r''(4.056) = < −1.288, −11.88 >`

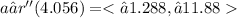
4.

The speed of the skier when he is at his maximum height and find his speed in meters/min.

The y-component of the vector function is given by
`y = (15 − t)(1 − sin(t))`

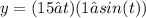
To find the maximum height, we differentiate the function and set it equal to 0:

`dy/dt = -sin(t) + t cos(t) - 14 = 0`

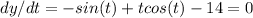
At maximum height, the y-component of the velocity vector is zero, hence,

`y'(t) = -15cos(t) + tcos(t) - 1 + sin(t) = 0At y'(t) = 0, cos(t) = 1/15 and sin(t) = √(224)/15`

The maximum height is then:

`y = (15 − t)(1 − sin(t)) ≈ 16.965 m`

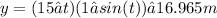
At maximum height, the velocity of the skier is given by the magnitude of the velocity vector

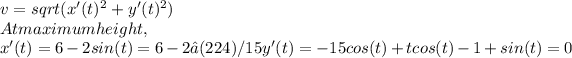`v = sqrt(x'(t)^2 + y'(t)^2)\\At maximum height,\\ x'(t) = 6 - 2sin(t) = 6 - 2√(224)/15y'(t) = -15cos(t) + tcos(t) - 1 + sin(t) = 0`The velocity is:

`v ≈ sqrt(108 + 224/25) ≈ 11.45 m/min`

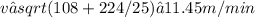
F4.5.

The total distance in meters that the skier travels from t = 0 to t = 15 minutesThe total distance of the skier's path from t = 0 to t = 15 minutes can be found by integrating the magnitude of the derivative of the vector function over the given time interval.

Let's compute the integral:

`∫|r'(t)|dt = ∫sqrt(x'(t)^2 + y'(t)^2)dt = ∫sqrt((6-2sin(t))^2 + (-15cos(t) + tcos(t) - 1 + sin(t))^2)dt`

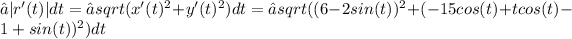
for 0 ≤ t ≤ 15 minutes

Let's use a numerical integration method, such as the trapezoidal rule, to approximate the integral. The formula for the trapezoidal rule is given by:

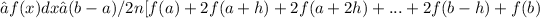`∫f(x)dx ≈ (b-a)/2n [f(a) + 2f(a+h) + 2f(a+2h) + ... + 2f(b-h) + f(b)`]where a = 0, b = 15 and n = 100

.h = (b-a)/n = 15/100 = 0.15Using a spreadsheet or Python code to evaluate the integrand for t = 0, 0.15, 0.30, ..., 14.85, 15 and applying the trapezoidal rule formula, we get:

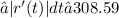`∫|r'(t)|dt ≈ 308.59` meters (rounded to two decimal places)

1. The slope of the path at time t = 4 is 3.752.

The time when the skier's horizontal position is x = 60 is t ≈ 4.056 minutes.3. The acceleration vector of the skier when the skier's horizontal position is
`x = 60 is ≈ < −1.288, −11.88 >`

4. The speed of the skier when he is at his maximum height is ≈ 11.45 m/min.5. The total distance in meters that the skier travels from t = 0 to t = 15 minutes is ≈ 308.59 meters.

Thus, we have found the answers for each question and the total distance travelled by the skier over the given time interval is approximately 308.59 meters.