Question

A sample of gas at a constant volume initially has a temperature of 315.0 K with a pressure of 2.50 atm. The temperature changes to 150.0 K. Calculate the final pressure.

Answer 1

The final pressure will be approximately 1.19 atm when the temperature changes from 315.0 K to 150.0 K, holding the volume constant.

To solve this problem, we can use Charles' Law, which states that, at constant volume, the pressure and temperature of a gas are directly proportional.

The formula we will use is:

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{(P_1)/(T_1 )=(P_2)/(T_2) } \end{gathered}$} }`

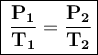
Where:

• P₁ = initial pressure = 2.50 atm
• T₁ = initial temperature = 315.0 K
• T₂ = temperature = 150.0 K
• P₂ = final pressure = ?

Solving the formula for V₂:

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{P_2=(P_1T_2)/( T_1) } \end{gathered}$} }`

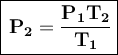
Where:

• P₁ = initial pressure
• T₁ = initial temperature
• T₂ = temperature
• P₂ = final pressure

We substitute the known values:

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{P_2=\frac{2.50 \ atm*150.0\\ot{K} }{315.0\\ot{k} } } \end{gathered}$} }`

`\boxed{\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{P_2\approx1.19 \ atm } \end{gathered}$} }}`

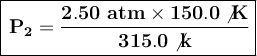
The final pressure will be approximately 1.19 atm when the temperature changes from 315.0 K to 150.0 K, holding the volume constant.