Question

A gas has a volume of 50.0 mL at a temperature of 10.0 K and a pressure of 760. kPa. What will be the new volume when the temperature is changed to 20.0 K and the pressure is changed to 380. kPa?

Answer 1

When the temperature changes to 20.0 K and the pressure changes to 380 kPa, the new volume will be approximately 0.2 L (200.0 mL).

To solve this problem using the gas laws, we need to use the Ideal Gas Law. This law states that the product of the pressure and the volume of a gas is proportional to the absolute temperature.

The equation of the Ideal Gas Law is the following:

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{(P_1V_1)/(T_1)=(P_2V_2)/(T_2) } \end{gathered}$} }`

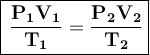
Where:

• P₁ = initial pressure = 760 kPa
• V₁ = initial volume = 50.0 mL = 0.050 L
• T₁ = initial temperature = 10.0 K
• P₂ = Final pressure = 380 kPa
• T₂ = final temperature = 20.0 K
• V₂ = Final volume = ?

We clear for V₂:

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{V_2=(P_1V_1T_2)/(P_2T_1 ) } \end{gathered}$} }`

Where:

• P₁ = initial pressure
• V₁ = initial volume
• T₁ = initial temperature
• P₂ = Final pressure
• T₂ = final temperature
• V₂ = Final volume

Substituting the known values:

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{V_2=\frac{760\\ot{kPa}*0.050 \ L*20.0\\ot{k} }{ 380\\ot{kPa}*10.0\\ot{k} } } \end{gathered}$} }`

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{V_2=(760 \ L)/(3800 ) } \end{gathered}$} }`

`\boxed{\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{V_2\approx0.2 \ Liters} \end{gathered}$} }}`

When the temperature changes to 20.0 K and the pressure changes to 380 kPa, the new volume will be approximately 0.2 L (200.0 mL).