Question

Please help!!! Thank you

Answer 1

Check the picture below.

so the parabolic path of the disc is pretty much like that one below. When does it reach its maximum height? well heck is just at the vertex, so let's find its vertex anyway.

`\textit{vertex of a vertical parabola, using coefficients} \\\\ y=\stackrel{\stackrel{a}{\downarrow }}{-16}x^2\stackrel{\stackrel{b}{\downarrow }}{+20}x\stackrel{\stackrel{c}{\downarrow }}{+6} \qquad \qquad \left(-\cfrac{ b}{2 a}~~~~ ,~~~~ c-\cfrac{ b^2}{4 a}\right)`

`\left(-\cfrac{ 20}{2(-16)}~~~~ ,~~~~ 6-\cfrac{ (20)^2}{4(-16)}\right) \implies\left( - \cfrac{ 20 }{ -32 }~~,~~6 - \cfrac{ 400 }{ -64 } \right) \\\\\\ \left( \cfrac{ 20 }{ 32 }~~,~~6 + \cfrac{ 25 }{ 4 } \right)\implies \left( \cfrac{ 20 }{ 32 }~~,~~\cfrac{49}{4} \right)\implies \stackrel{seconds\qquad feet }{(~0.625~~,~~ 12.25~)}`

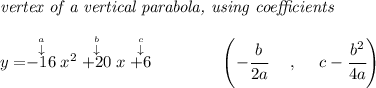
how long is it when it's 3 feet off the ground?

or

what's "x" when h = 3?

`\stackrel{h}{3}=-16t^2+20t+6\implies 0=-16t^2+20t+3 \\\\\\ ~~~~~~~~~~~~\textit{quadratic formula} \\\\ 0=\stackrel{\stackrel{a}{\downarrow }}{-16}t^2\stackrel{\stackrel{b}{\downarrow }}{+20}t\stackrel{\stackrel{c}{\downarrow }}{+3} \qquad \qquad t= \cfrac{ - b \pm \sqrt { b^2 -4 a c}}{2 a} \\\\\\ t= \cfrac{ - (20) \pm \sqrt { (20)^2 -4(-16)(3)}}{2(-16)} \implies t = \cfrac{ -20 \pm \sqrt { 400 +192}}{ -32 }`

`t= \cfrac{ -20 \pm \sqrt { 592 }}{ -32 }\implies t= \cfrac{ -20 \pm 4\sqrt { 37 }}{ -32 }\implies t= \cfrac{ -5 \pm \sqrt { 37 }}{ -8 } \\\\\\ t= \cfrac{ 5 \mp \sqrt { 37 }}{ 8 }\implies t\approx \begin{cases} -0.14\\\\ ~~ 1.39~seconds ~~ \textit{\LARGE \checkmark} \end{cases}`

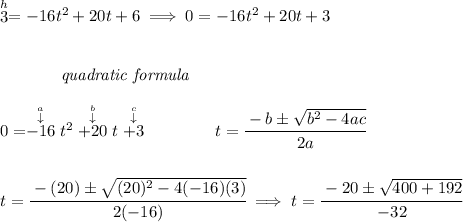
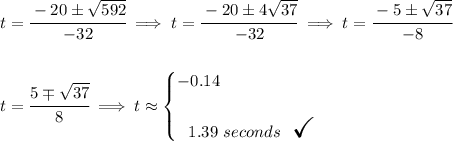
now, we can't use the negative value of "t", because the seconds in this case can't be negative.