The estimated probability that the frog jumps off the board within 60 seconds based on the three repetitions of the frog's jumps is approximately 0.6667 or 66.67%.
In the provided random number table, the numbers are used to simulate the frog's jumps. To calculate the estimated probability of the frog jumping off the board within 60 seconds, we count the number of occurrences where the random numbers are less than or equal to the given threshold.
In each repetition, the threshold for a jump within 60 seconds is 60,000. For the first repetition, the counts of numbers less than or equal to 60,000 are 6. In the second repetition, there are 8 such numbers, and in the third repetition, there are 7. Adding these counts together (6 + 8 + 7), we get a total of 21 successful jumps within 60 seconds out of the 30 total jumps simulated (3 repetitions × 10 jumps each).
The estimated probability (P) is then calculated as the ratio of successful jumps to total jumps:
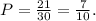Converting this to a percentage gives us approximately 66.67%. Therefore, based on the simulation, there is a 66.67% chance that the frog will jump off the board within 60 seconds.
This approach uses the random numbers to model the randomness of the frog's jumps and provides an estimate of the probability based on the simulated outcomes.