Question

There are 4 white marbles,6 red marbles,and 2 blue marbles.Once a marble is selected,it is not replaced.Find the probability of selecting 2 blue marbles.

Answer 1

There are 4 white marbles,6 red marbles, and 2 blue marbles. Once a marble is selected,it is not replaced.Find the probability of selecting 2 blue marbles. --- # of ways to succeed: 2C2 = 1 --- # of random pairs: 12C2 = 66 --- P (2 blue) = 1/66

Answer 2

`(1)/(66) \approx 1.5\%`

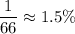
Explanation:

Probability is a measure of the likelihood or chance that a specific event or outcome will occur.

`\boxed{\sf Probability\:of\:an\:event\:occurring = (Number\:of\:ways\:it\:can\:occur)/(Total\:number\:of\:possible\:outcomes)}`

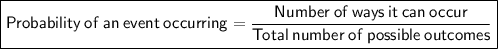
We are told that there are 4 white marbles, 6 red marbles and 2 blue marbles. Therefore, the probability of selecting a blue marble on the first pick is:

`\sf P(blue\;1st)=(2)/(4+6+2)=(2)/(12)=(1)/(6)`

As the first marble selected is not replaced, we now have 1 blue marble remaining, and a total of 11 marbles remaining.

Therefore, the probability of selecting a blue marble on the second pick is:

`\sf P(blue\;2nd)=(1)/(11)`

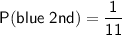
To calculate the probability of both events occurring (selecting 2 blue marbles), we multiply the probabilities:

`\sf P(blue\;1st)\;and\;P(blue\;2nd)=(1)/(6) * (1)/(11)=(1)/(66)`

Therefore, the probability of selecting 2 blue marbles without replacement is 1/66 ≈ 1.5%.