Question

The quadratic equation 3x2-x+ k = kx-1, where k is a constant, has two distinct roots. Find the range of values of k.

please help me with this question..thank you​

Answer 1

k < -1 or k > 11

Explanation:

Given quadratic equation:

`3x^2-x+ k = kx-1`

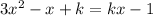
First, rearrange the given quadratic equation in standard form ax² + bx + c = 0:

`\begin{aligned}3x^2-x+ k &= kx-1\\3x^2-x+ k-kx+1&=0-kx+1\\3x^2-x-kx+ k+1&=0\\3x^2-(1+k)x+ (k+1)&=0\end{aligned}`

`3x^2-(1+k)x+ (k+1)=0`

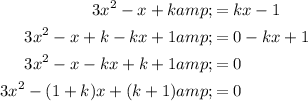
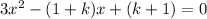
Comparing this with the standard form, the coefficients a, b and c are:

• a = 3
• b = -(1 + k) = (-1 - k)
• c = (k + 1)

`\boxed{\begin{minipage}{7 cm}\underline{Discriminant}\\\\$\boxed{b^2-4ac}$ \quad when $ax^2+bx+c=0$\\\\when $b^2-4ac > 0 \implies$ two real roots.\\when $b^2-4ac=0 \implies$ one real root.\\when $b^2-4ac < 0 \implies$ no real roots.\\\end{minipage}}`

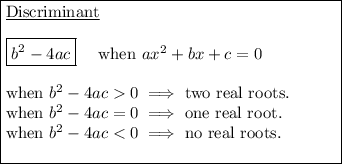
If the quadratic equation has two distinct roots, its discriminant is positive.

`b^2-4ac > 0`

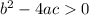
Substitute the values of a, b and c into the discriminant:

`(-1 - k)^2-4(3)(k+1) > 0`

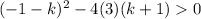
Simplify:

`(-1 - k)(-1-k)-12(k+1) > 0`

`1+2k+k^2-12k-12 > 0`

`k^2+2k-12k+1-12 > 0`

`k^2-10k-11 > 0`

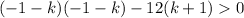
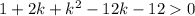
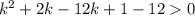
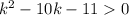
Factor the left side of the inequality:

`k^2+k-11k-11 > 0`

`k(k+1)-11(k+1) > 0`

`(k-11)(k-1) > 0`

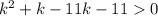
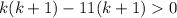
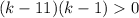
If we graph the quadratic k² - 10k - 11, it is a parabola that opens upwards (since its leading coefficient is positive), and crosses the x-axis at k = -1 and k = 11. Therefore, the curve will be positive (above the x-axis) either side of the x-intercepts, so when k < -1 or k > 11.

Therefore, the range of values of k for which the given quadratic equation has two distinct roots is:

`\boxed{k < -1 \; \textsf{or} \;k > 11}`