Question

Please help me with question 25. And please include an explanation.

Answer 1

`\Huge \boxed{\Florin f(x) = 2x^(3) - 8x^(2) + 6x}`

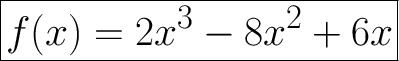
Step 1: Identify the zeros

The given zeros are 0, 1, and 3.

Step 2: Write the factors

Since the zeros are the values of
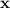`\bold{x}` that make the polynomial equal to zero, we can write the factors corresponding to each zero as
`(x - 0)`,
`(x - 1)`, and
`(x - 3)`.

Simplifying the first factor, we get
`(x)`,
`(x - 1)`, and
`(x - 3)`.

Step 3: Multiply the factors

Now, multiply the factors together to form the polynomial:

`\Large \boxed{(x)(x - 1)(x - 3)}`

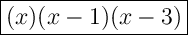
Expanding this expression, we get:

`\Large \boxed{x^(3) - 4x^(2) + 3x }`

Step 4: Apply the leading coefficient

The leading coefficient is 2, so we need to multiply the entire polynomial by 2:

`\Large \boxed{2(x^(3) - 4x^(2) + 3x)}`

Expanding this expression, we get:

`\Large \boxed{2x^(3) - 8x^(2) + 6x}`

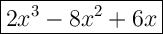
Step 5: Answer

So, the polynomial function in standard form with a leading coefficient of 2 and zeros at 0, 1, and 3 is:

`\large \boxed{\Florin f(x) = 2x^(3) - 8x^(2) + 6x}`

________________________________________________________