Final Answer:
Part A:

Part B:

Part C:
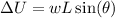
Step-by-step explanation:
In Part A, the work done by the force of friction
 can be expressed as
can be expressed as
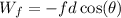 , where f is the force of friction. Since
, where f is the force of friction. Since
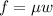 and the displacement d is L , the expression becomes
and the displacement d is L , the expression becomes
 , where the negative sign indicates the opposing direction of the force of friction.
, where the negative sign indicates the opposing direction of the force of friction.
For Part B, the work done by the applied force W is the sum of the work done by the applied force and the work done against friction. The applied force contributes
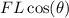 to the work, and the force of friction contributes
to the work, and the force of friction contributes
 , resulting in the expression
, resulting in the expression
 .
.
In Part C, the change in potential energy
 is related to the change in height of the block. As the block is pushed up the incline, the change in height is
is related to the change in height of the block. As the block is pushed up the incline, the change in height is
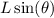 , and since potential energy is given by U = mgh , where m is mass and g is the acceleration due to gravity,
, and since potential energy is given by U = mgh , where m is mass and g is the acceleration due to gravity,
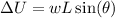 .
.
Therefore, the final expressions for the three parts are
 ,
,
 , and
, and
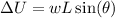 .
.