Question

NO LINKS!! URGENT HELP PLEASE!!!

O is the center of the regular decagon below. Find its perimeter. Round to the nearest tenth if necessary.

Answer 1

65.0 units

Explanation:

A regular decagon is a 10-sided polygon with sides of equal length.

To find its perimeter, we first need to find its side length (s).

As we have been given its apothem, we can use the apothem formula to find an expression for side length (s).

`\boxed{\begin{minipage}{5.5cm}\underline{Apothem of a regular polygon}\\\\$a=(s)/(2 \tan\left((180^(\circ))/(n)\right))$\\\\where:\\\phantom{ww}$\bullet$ $s$ is the side length.\\ \phantom{ww}$\bullet$ $n$ is the number of sides.\\\end{minipage}}`

Given the apothem is 10 units and the number of sides is 10, substitute a = 10 and n = 10 into the formula and solve for s:

`10=(s)/(2 \tan \left((180^(\circ))/(10)\right))`

`10=(s)/(2 \tan \left(18^(\circ)\right))`

`s=20 \tan \left(18^(\circ)\right)`

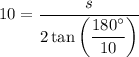
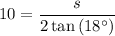
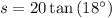
The perimeter (P) of a regular polygon is the product of its side length and the number of sides. Therefore, the perimeter of the given regular decagon is:

`P=s \cdot n`

`P=20 \tan \left(18^(\circ)\right) \cdot 10`

`P=200 \tan \left(18^(\circ)\right)`

`P=64.9839392...`

`P=65.0\; \sf units\;(nearest\;tenth)`

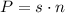
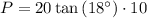
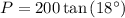
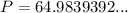
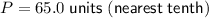
Therefore, the perimeter of a regular decagon with an apothem of 10 units is 65.0 units, to the nearest tenth.

Answer 2

65 units

Explanation:

solution Given:

apothem(a)=10

no of side(n)= 10

First, we need to find the length of one side (s).

We can find the length of one side using the following formula:

`\boxed{\bold{s = 2 * a * tan((\pi)/(n))}}`

substituting value:

`\bold{s = 2 * 10 * tan((\pi)/(10))=6.498}` here π is 180°

Now

Perimeter: n*s

substituting value:

Perimeter = 10*6.498= 64.98 in nearest tenth 65 units

Therefore, the Perimeter of a regular decagon is 65 units.