Question

Solve the system of equations x-y=-1 and x+8y=35 by combining the equations

Answer 1

(x, y) = (3, 4)

Explanation:

You want to solve the system of equations by combining the equations:

• x -y = -1
• x +8y = 35

Observation

The coefficients of x have the same value (1), so we can eliminate x by multiplying one of the equations by -1 and adding the result. Since we want the resulting coefficient of y to be positive, we choose to multiply the first equation by -1.

`\begin{array}{c,l,l,l}-1&(x&-y&=-1)\\+1&(x&+8y&=35\,)\end{array}`

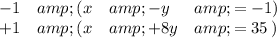
Combined equations

Then the sum is ...

`\begin{array}{rcl}-x&+y&=1\\x&+8y&=35\\\cline{1-3}0x&+9y&=36\end{array}`

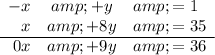
Solution

The solution to this is ...

y = 36/9 = 4

x = y -1 = 4 -1 = 3 . . . . . . from the first equation

The solution is (x, y) = (3, 4).

<95141404393>