Question

1. Two functions f(x) and g(x) are defined on the set of real numbers by f(x) = 3x²

2 − 2, and g(x) = x+3. Find : (i) f(-2)
(ii) g−1( − 2);
(iii) the value of x for which f[g(x)] = g[f(x)]
(iv) f−1[g(4)]

Answer 1

Here are the steps to find the values:

(i) To find f(-2), substitute -2 into the function f(x):

`\sf\: f(-2) = 3(-2)^2 - 2 \\ \sf\: f(-2) = 3(4) - 2 \\ \sf\: f(-2) = 12 - 2 \\ \sf\: f(-2) = 10`

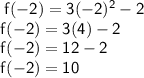
Therefore, f(-2) = 10.

(ii) To find g⁻¹(-2), we need to find the value of x that satisfies g(x) = -2.

`\sf\: g(x) = x + 3 \\ \sf\: -2 = x + 3 \\ \sf\: x = -2 - 3 \\ \sf\: x = -5`

Therefore, g⁻¹(-2) = -5.

(iii) To find the value of x for which f[g(x)] = g[f(x)], we need to set the two functions equal to each other and solve for x:

`\sf\: f[g(x)] = g[f(x)] \\ \sf\: 3[g(x)]^2 - 2 = g(x) + 3 \\ \sf\: 3(x + 3)^2 - 2 = x + 3 \\ \sf\: 3(x^2 + 6x + 9) - 2 = x + 3 \\ \sf\: 3x^2 + 18x + 27 - 2 = x + 3 \\ \sf\: 3x^2 + 17x + 25 = x + 3 \\ \sf\: 3x^2 + 16x + 22 = 0`

You can then solve this quadratic equation to find the value(s) of x.

(iv) To find f⁻¹[g(4)], we need to find the value of x that satisfies f(x) = 4.

`\sf\: f(x) = 3x^2 - 2 \\ \sf\: 4 = 3x^2 - 2 \\ \sf\: 3x^2 = 6 \\ \sf\: x^2 = 2 \\ \sf\: x = \pm √(2)`

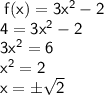
Therefore, f⁻¹[g(4)] = ±√2.