Question

A small company borrows money and remains in debt to its lenders for a period of time. The function f(x)=-8x^2+8x+50 represents the amount of debt the company has, in thousands of dollars, x years after opening its business.

Approximately how many years after opening its business will the company be out of debt?
3.3 years
3.7 years
3.1 years
3.5 years

Answer 1

Answer: 3.1 years (choice C)

===============================================

Work Shown:

x = number of years, some positive real number

f(x) = debt level in thousands of dollars

The company is out of debt when f(x) = 0

We go from

f(x)=-8x^2+8x+50

to

0 = -8x^2+8x+50

We'll use the quadratic formula to solve.

Plug in: a = -8, b = 8, c = 50

`x = (-b\pm√(b^2-4ac))/(2a)\\\\x = (-8\pm√(8^2-4(-8)(50)))/(2*(-8))\\\\x = (-8\pm√(1664))/(-16)\\\\x = (-8+√(1664))/(-16) \ \text{ or } \ x = (-8-√(1664))/(-16)\\\\x \approx -2.0495\ \text{ or } \ x \approx 3.0495\\\\x \approx -2.1\ \text{ or } \ x \approx 3.1\\\\`

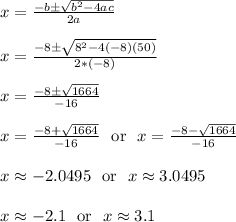
Ignore the negative x value. It doesn't make sense to have a negative number of years.

The only practical solution is approximately 3.1 years.